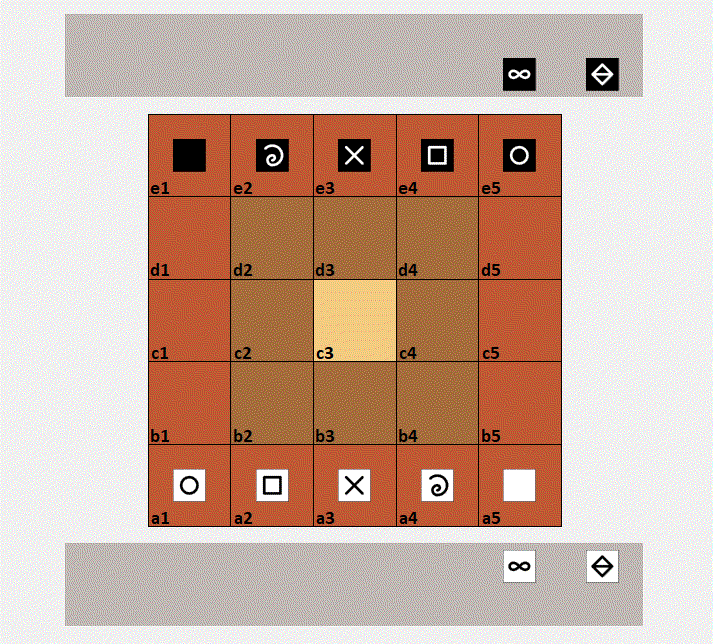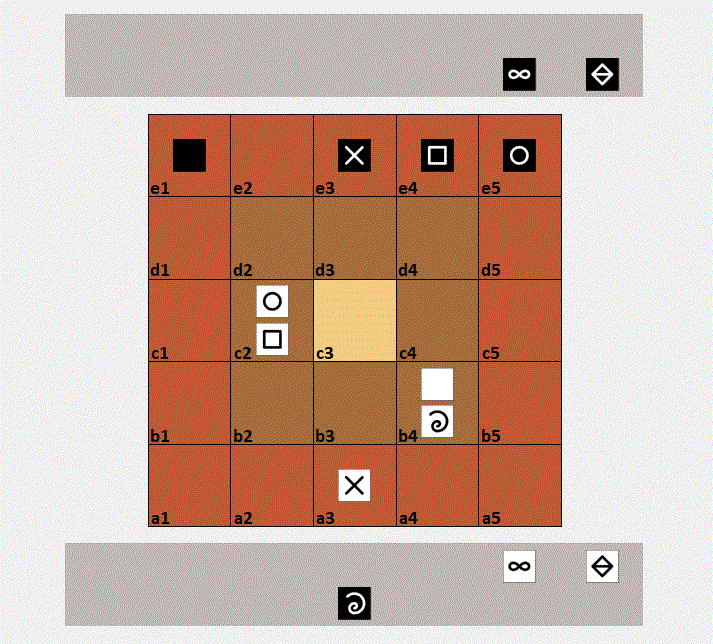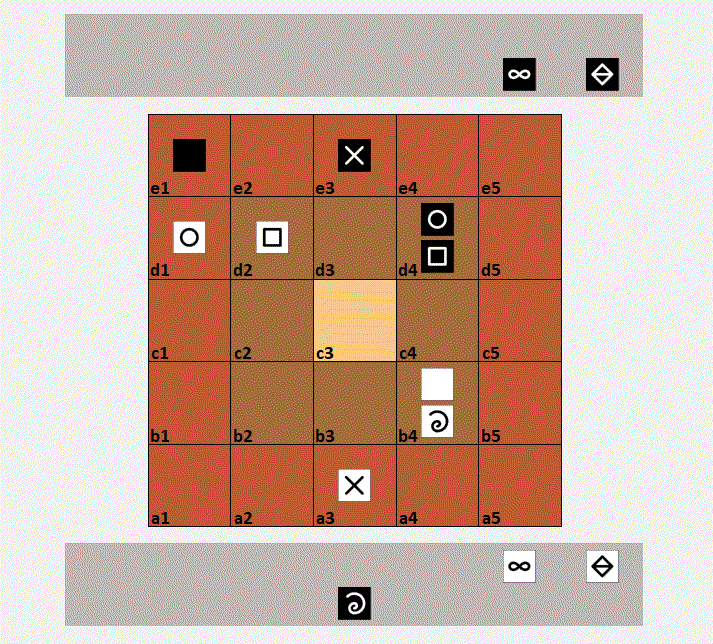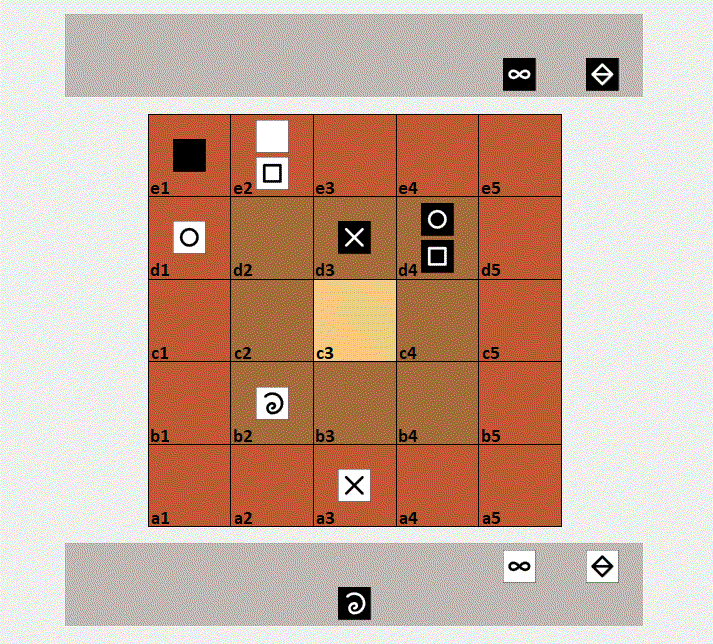
Mikjersi describes the rules of a micro-variant of the Jersi board-game.
The rules of Mikjersi are those of Jersi, but with the following major changes:
- Board -- The board is made of 5x5 squared cells.
- Moves -- The moves are only vertically and horizontally, but not along diagonal.
- Cubes -- Each player owns 7 cubes: rock, paper, scissors, fool, king, mountain and wise.
The complete rules of Mikjersi can be found in the booklet either in English or in French.
Above an animated game play from two AI agents of the sister project mikjersi-certu.