Inner Product Space Characterization by Isometry Group over Unity Sphere
Par Lucas le dimanche 1 décembre 2013, 19:08 - Mathématiques - Lien permanent
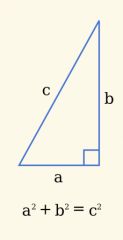
Why “power 2” in the Pythagorean theorem ?
Let us assume a geometry over the set E considered as 1) a vector space over the real field ; 2) with finite dimensions ; 3) equiped with a norm.
Which additional axioms have to be added in order to conclude that E is euclidean, or equivalently, that its norm is deriving from an inner product. Such additionnal axioms are searched in topology and in group formulations, as opposed to calculational ones, like the “polarisation identity”.
The attached document gathers theorems that proof the following axiom solution: 4) if a group G of isometries allows transportation between any pair of points of the unity sphere of E, then E is euclidean.
Borboleta_2013_Inner-Product-Space-Characterization-by-Isometric-Group-over-Unity-Sphere.pdf